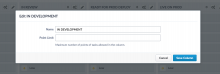
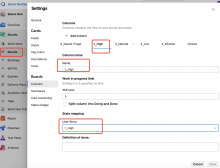
Project boards currently support changing task status and task priority via triggers.
Unfortunately, there is no way to achieve the inverse. This makes it necessary to drag the task across the board, or otherwise the status / priority will get out of sync.
This kind of one way behavior is very unintuitive for many users.
I therefore propose that we create some way of automation for moving tasks between columns based on status changes and priority changes. There are several approaches I can think of for solving this, but they have all different pros and cons.
- making some of the trigger actions bidirectional: The advantage of this is that it's extremely simple to set up. Preferably, this would be a checkbox and could be easily added by administrators to existing project boards. Disadvantage would be, that this is pretty much against the design of column triggers and probably would make the implementation of triggers quite convoluted.
- adding automations for columns: pretty much the inverse of a trigger. I imagine something like Github project automations. The advantage would be that this is very similar to triggers and users would probably understand how to set it up. Disadvantage would be that this adds an additional concept and system to projects and makes them more complex.
- create Herald action for changing project column: The advantage of this would be that it's probably 100% inline with how Phabricator does things and would perhaps be the simplest way to make this possible. A disadvantage of this approach is the wide separation of triggers and automation, which could make it hard for users and new administrators to understand.
This is a similar task from the original project: https://secure.phabricator.com/T6409